|
ABF305 Investment Management
Lecture 12
In this lecture, we will:
在本次讲座中,我们将:
Cover the risk-return trade off:
覆盖风险回报权衡:
Chapter 5 in the textbook, specifically pages 113-128 and pages 130-132.
在课本的第5章,特别是第113-128页,第130-132页。
Risk-return trade off.
风险收益权衡。
If you want a higher return for an investment, then you should expect to pay a price for this in terms of accepting a higher investment risk.
如果你想有一个更高的投资回报,那么你应该想到为此付出一定的代价,接受较高的投资风险。
The risk return trade-off or relationship can be represented by an equilibrium.
可以表示为一个平衡的风险回报权衡关系。
Markowitz and Sharpe have addressed the risk-return relationship in modern portfolio theory.
马科维茨,夏普已经解决了现代投资组合理论中的风险与回报的关系。
Need measurements of:
需要测量:
The return of the asset.
资产的回报。
The risk of an asset.
资产的风险。
The quantitative trade-off between risk and expected return.
定量风险与预期回报之间的权衡。
The return of an asset.
For stocks, the way to determine the rate of return, is from the dividend paid and also the capital gain or loss on the stock price.
For example: If a stock costs $25 and after a year the price has changed to $27.80. In addition, you received a dividend of 40 cents for the stock at the end of the year. Then your percentage return is (27.80+0.40-25)/25 = (3.2/25) =12.8%
Issues to consider!
The customary method of arriving at stock returns is a year-to-year historical rate of return using historical data, namely the stock price.
However, hypothetically, expected return can be used which are adjusted for the probability of state of economy.
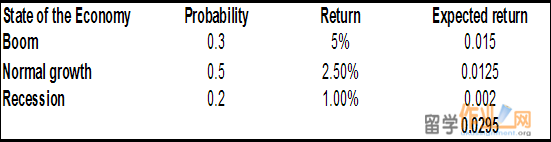
Effective annual return or EAR.
If you do not hold the shares for 1 year, then you will need to adjust the return accordingly. Let us say that you bought a share for $18 and held it for 3 months after which the price was $19; you received no dividend. Your holding period percentage return for three months is determined as 19-18/18 = 0.0555 or 5.56%.
1+EAR = (1.0556)^4 = 1.2416 so the effective annual return is 24.16%.
The risk of an asset.*
If risk is thought of in terms of the volatility of an asset’s returns, to quantify this risk, the return variance and standard deviation are employed. Specifically, variance and its square root which is known as the standard deviation, are the most commonly used measures of volatility. Remember volatility is unpredictability. The degree of movement of difference from an average return therefore represents a measure of just how unpredictable a return is. *
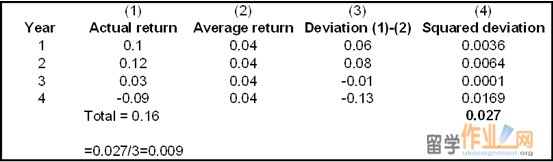
How to calculate standard deviation.
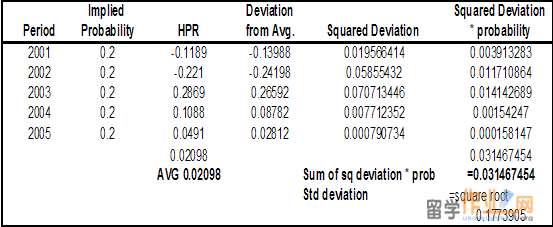
If we were to employ the scenario in which we use the probability of a return occurrence is not equal to one
With an average return measure and standard deviation, employing a normal distribution which employs for these measures will tell you the probability of your return ending up in a given range.
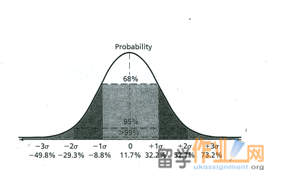
In this example, a return mean is determined as 11.7% for a stock, and the standard deviation 20.5%. Given that 1 standard deviation around the mean represents a 68% probability or a 2/3 chance of an occurrence, we can deduce that for our stock, should we decide to purchase it, then we can expect a return which will fall within a range of 11.7+/-20.5% which is between 32.2% and -8.8%.
Pop quiz to see your understanding:*
Given a data series that is normally distributed with a mean of 100 and a standard deviation of 10, about 95 percent of the numbers in the series will fall within which of the following ranges?
a. 60 to 140 b. 70 to 130 c. 80 to 120 d. 90 to 110
What do we mean by data series by the way?
The answer is: c
On the normal distribution, a 95 percent probability of occurrence is represented by 2 standard deviations. The range then given a mean of 100 and a standard deviation of 10 is 100 +/- (2 x 10) = 80 to 120 so the answer is c.
Pop quiz to see your understanding:*
The average return for Firm X is 20%, the standard deviation is 10%. Assuming the returns are normally distributed, what is the probability that Firm X will yield a negative return?
a. 17% b. 33% c. 5% d. 2.5%
The answer is: d
If the average is 20%, then to realize a negative return, the return must be less than 0%. For a 0% return to occur, this is two standard deviations away from the average, namely 2 x -10%.
If 2 standard deviations around the mean = 95% then to fall out with the 95%, it occurs 5%, and to fall below the 0%, then that must be 5%/2 = 2.5% so the answer is d.
Qualification:
With this formula, you need to be careful though in employing it. Firstly you need to use decimals and not percentages, and in addition this formula only works if the returns come from a normal distribution.
Both are appropriate:
The geometric average tells you what you actually earned per year on average, compounded annually.
The arithmetic average tells you what you earned in a typical year.
Usually when reference is made to an average return, it is the average arithmetic return, however, unless otherwise stated.
Group assignment:
Work out returns and standard deviations.
Also explain in your own words the concept ‘utility value’. While utility value will be covered in next week’s lecture, for the assignment, the idea is to get you to do some preparation beforehand.
Summary of what we know:
We can quantify return and risk for a single stock.
What about a portfolio?
|






