|
Assignment 1:
Queues & Simulation Systems (QSS) develops software systems for queuing models and simulation studies. The company operates a technical support for its customers. A customer may call the technical support center for consultation, if he/she has problems whatsoever with the software offered by the company. QSS has expanded the support center and operates at this point with two consultants. If both consultants are busy, when a call arrives, the caller hears a recorded message stating that all consultants are busy with other customers. The customer is then asked to hold and told that a consultant will provide assistance as soon as possible. Customer calls follow a Poisson distribution with a mean arrival rate of 12 calls per hour. The service time follows an exponential distribution with a mean equal to 8 minutes. QSS扩大了支持中心,工作在这一点上与两名顾问。如果两个顾问都很忙,当呼叫到达时,主叫方听到录制的消息,指出所有的顾问都忙于其他客户。这样,客户便要求去把握和告诉记者,顾问会尽快提供协助。客户来电遵循泊松分布为每小时12呼叫平均到达率。服务时间服从指数分布,均值等于8分钟。
Answer the following questions using queuing theory: 答案使用排队论以下问题:
一个。什么是利用两个发球的平均率是多少?
湾多长的意思是顾客花费在排队?
角多长的意思是顾客的花费在系统中?
什么是客户等待顾问的平均数?
什么是用户在系统中的平均数目?
验证中的一个适当的仿真模型的结果而言上述答案。
a. What is the average rate of utilization of two serves?
b. How long does the mean customer spend in queue?
c. How long does the mean customer spend in the system?
d. What is the average number of customers waiting for a consultant?
e. What is the average number of customers in the system?
f. Verify the above answers in terms of the outcome of an appropriate simulation model.
QSS has recently received several letters from customers complaining about the difficulty in getting access to support. Management decides for this reason that the average customer should not have to wait for technical support for more than 2 minutes.
g. Does your analysis above support the claim that QSS already fulfills these requirements?
h. What actions – if any – would you recommend?
QSS decides to investigate the impact of using a third consultant at its support center.
i. Answer questions a.-e. given that three consultants are available in the support center.
j. Verify your answer to Question i. in terms of the outcome of an appropriate simulation model.
Kingman’s equation generalizes the computation of waiting time in queue from the M/M/m model to a model with general interarrival and service time distributions. k. Verify this result in terms of a simulation study for the above M/M/2 and M/M/3 models with
Poisson arrivals and exponential service times replaced by some distributions after your own choice.
Assignment 2:
A manufacturing firm produces and sells a product to a single independent retailer. The product is sold during a single selling season. The manufacturer has production cost is $5.00 per unit and the retailer sells the product to the consumers at a price of $20.00 per unit. Unsold units at the end of the selling season have a salvage value of $4.00. If the retailer cannot meet the demand during the selling season then she has a goodwill penalty cost of $1.00 and the manufacturer has an equivalent goodwill penalty cost of $1.00. To procure the product the retailer has a cost of $1.00 per unit. The retailer places an order with the manufacturer at the start of the selling season and the delivery is instantaneous. The consumer demand follows a beta distribution with shape parameter
1α = and 2β = and a range between a=0 and b=250.

B) Suppose that the supply chain members make joint decisions.
1. Which order quantity is the optimal for the supply chain?
2. What is the optimal supply chain profit?
C) The manufacturer offers the retailer a wholesale-price contract with a wholesale price of $12.00 per unit.
1. Find an optimal order quantity for the retailer.
2. Based on the retailer’s optimal order quantity, then what are the profits for the individual members of the supply chain and what is the profit for the supply chain?
3. Construct a diagram showing the individual members profit as well as the supply chain profit as a function of the retailer’s order size.
D) The manufacturer now offers a revenue-sharing contract with a wholesale price of $8.00, but where the retailer only keeps 75% of her revenue.
1. Find an optimal order quantity for the retailer.
2. Based on the retailer’s optimal order quantity, then what are the profits for the individual members of the supply chain and what is the profit for the supply chain?
3. Construct a diagram showing the individual members profit as well as the supply chain profit as a function of the retailer’s order size.
4. Compare the results in D.1-D.3 with the results of C.1-C.3.
5. Is the revenue-sharing contract offered by the manufacturer a coordinating contract for the supply chain? Argue why or why not.
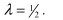
E) The manufacturer now offers a revenue-sharing contract satisfying the equations at the bottom of page 246 in Cachon where
1. Identify the resulting wholesale price as well as the fraction of revenue which the retailer should keep.
2. Find an optimal order quantity for the retailer using the wholesale price and the fraction of revenue which the retailer should keep found in question E.1.
3. Construct a diagram showing the individual members profit as well as the supply chain profit as a function of the retailer’s order size.
4. Is the revenue-sharing contract offered by the manufacturer a coordinating contract for the supply chain? Argue why or why not.
F) Besides the revenue-sharing contract the manufacturer and the retailer has also been negotiating a quantity-discount contract.
1. Discuss whether or not it may be better to use a quantity-discount contract than a revenue-sharing contract in practice.
2. The manufacturer offers the following wholesale price (discount) function:
 |
 |
|||
| 网站地图 |

